注)私 t-dash は数学や物理、画像解析等に詳しいわけではなく、素人の知識と理解力しかありません(対数の底の変換公式をすっかり忘れていたぐらいです)。また、Photoshop を日常的に使うユーザでもありませんし、カメラにも詳しくないです。このページにはウソや勘違い、思い込みが力強く記述されている可能性がありますが、適切にフィルタリングしてご覧下さい。

Photoshop のフィルタ「ガウス」を使うと、ピンぼけ風の写真を簡単に作る事ができます。
たとえば右の写真に対してガウス処理を施してみます。

Photoshop のガウスフィルタを適用すると、たとえばこのような感じになります。
「はいっ、ピンぼけ写真のできあがり!」なのですが...
ですが、よく観察して見ると、カメラのぼけ方とは何かが違うようです。
Photoshop のぼかしフィルタ「ガウス」は、
指定されたサイズと定義された正規分布のパターンに従って、暗い部分も明るい部分も等しく周辺に広げます。
10値明るいものも10値暗いものも、その度合いを等しくプラスに、あるいはマイナスに扱います。
その結果、明るい部分と暗い部分が区別なく均一に綺麗に混ざり合い、均質にぼけたコントラストの下がった
画像が生成されます。
一方、カメラのフィルムやCCD、人の目の網膜の場合はどうでしょう。
大きく開いた絞りを通過した光がフィルム上で結像せずにぼやけた場合、その光は周辺の像と混ざり合い、フィルム上で加算されます。ここまではPhotoshopの処理と同じような感じです。
しかし、フィルムの感光剤やCCDの受光素子そして網膜の受光器官は、光のエネルギーを「対数的」にとらえているところが違います。
暗い部分の10値の差と明るい部分の10値の差は、光の強さの差が全く違っているはずです。
Photoshop のガウスフィルタは直線的に表現されたRGB値(通常それぞれは整数)で処理しています。
このPhotoshop のフィルタを、そのままカメラのぼけの表現を意図して使用(代用)するのは、「間違い」だと気付きました。
(この写真のぼけがものすごく不自然なのは、このせいでした。)
そこで、画像ファイルの各画素の RGB 値を、カメラのフィルムに当たる光の状態にまで戻し、つまりリニアな表現の RGB を指数変換し、その状態で周辺ピクセルとの演算を行って、「ピンぼけ」現象の再現実験をしてみました。

右の図は、各画素のリニアに表現されている RGB を指数変換し、対数表現的な状態に戻してぼかし処理を行い、その後さらに対数変換しリニアな RGB に戻したものです。
たったこれだけの処理で、カメラのぼけに近い雰囲気になりました。
さらに、周辺のピクセルをサンプルするマスクの形をいろいろ変えてみました。
ハイライトの強い部分が、絞りの形をまねて作った形になっているのをご覧頂けますでしょうか。
処理の流れの概要は次のような感じです。
- Photoshop でオリジナルイメージを「汎用フォーマット」形式の出力等を使って、自分のプログラムで扱いやすい形(たとえば RGB の列)で出力します。
- Photoshop で出力したファイルを読み込み、全ピクセルを指数変換します。以降、RGB は浮動小数点で扱います。
『Nm』 のNにどのような値を何を使うかで、最終的に得られる絵の雰囲気が大きくかわります。
(ピクセルの混ぜ合わせをしなければ 、Nにはどのような値(ただし 1<N)を入れても、RGB8ビットに戻した結果は元の絵と同じです。)
Nの値の選定には、好みにあわせたカットアンドトライが必要です。
実際に試してみたところ、N は 1.035 ぐらいが丁度良い感じです。1.1 ぐらいにすると明るくなり過ぎる感じです。
輝度が最大のとき、 N255ですので、変数がオーバーフローしないように浮動小数点変数の表現できる範囲に N の値をおさめる事も必要です。
(ちなみに、C 言語の float 型(32 ビット)は 3.4×1038、また double 型(64 ビット)は 1.7×10308 が表現の上限らしいです。)
現実の光学フィルム、CCD、網膜の特性に近い N の値が何なのかは、現在 t-dash は模索中で、よくわかっていません。
m は RGB のそれぞれの値です。
- イメージ内の全てのピクセルに対し、それぞれの近隣の(絞りを模したマスクに掛かる)ピクセルの値を均等に混ぜます。
(時間がかかる処理ですが、ここで高速フーリエ変換等を用いると処理を根本的に速くすることができます。)
-
全ピクセルを対数変換し、リニアな表現(Photoshop が扱う形式に)に変換し(戻し)ます。
このときの対数の底は先ほどの N です。
またRGBそれぞれ8ビットで表現できる範囲(0〜255)を超えた場合は、255でクリップします。
- 全ピクセルをRGB 各整数8ビットの列として出力します。
- 「汎用フォーマット」読み込みなどを利用してPhotoshopへ読み込みます。
処理手順は以上です。

|

|
|
N=1.01
|
N=1.03
|
上述の N の値を 1.01 〜 1.11 の間で変化させ、それぞれでぼかした画像をつくりました。
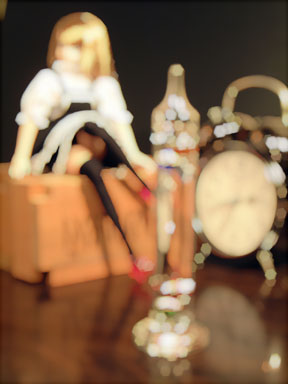
|
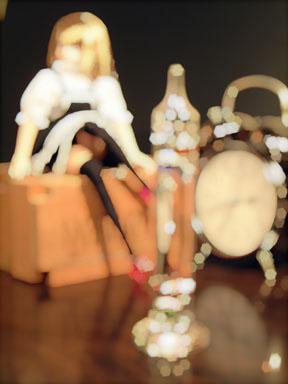
|
|
N=1.05
|
N=1.07
|

|

|
|
N=1.09
|
N=1.11
|
下の図は、ぼけた画像とオリジナル画像を Photoshop で単純合成したものです。

|

|
| Photoshop のガウスフィルタを使用した例 |
今回作ったフィルタを使用した例 |
Photoshop でアルファチャネルを追加し、そこに Z 値(奥行きの距離)的な値を作り、
その値に基づいてぼかしの絞り形状サイズを変化させ、かつZ値判定で上書き制御を行うと、本格的な浅い被写界深度のなめらかな画像を生成する事ができます。
まだ考察中の段階で、完成には至っていませんが、現状の仕上がり具合をご紹介します。

|

|
| オリジナルの画像 |
αチャネルに描き加えたZ(奥行き)情報 |
右のような画像に対し、ジャストフォーカスなZ値を変化させながら何枚か処理してみました(結果は下の画像)。
左側の絵は元画像、右側の絵は Photoshop のグラデーションツールを使って手作業で適当に描いたZ情報のイメージです。

|

|

|
| 31付近のZにフォーカス |
63付近のZにフォーカス |
95付近のZにフォーカス |

|

|

|
| 127付近のZにフォーカス |
159付近のZにフォーカス |
191付近のZにフォーカス |

|

|

|
| 223付近のZにフォーカス |
255付近のZにフォーカス |
|
対数表現に戻して処理する方法、単純な処理ですが結果は大きく違ったものになります。
Photoshop の次のバージョンには、ぜひ RGB の浮動小数点モードと対数表現モードが追加される事を期待します。
PC のビデオカードにも、約1678万色(=28x3)とかではなくて 、RGB を浮動小数点と対数で表現するビデオチップとメモリが搭載されると素晴らしいです。
8ビットの情報量しか持たないものを積和演算して再び8ビットに戻して...、の繰り返しでは、すぐに目立つレベルで演算誤差が現れ絵は荒れてしまいます。これが浮動小数点で表現される形式になるだけで、輝度差の少ない(たとえば暗い)シーンでも、ノイズの少ないきれいな画面になりそうです。
あるいはさらに対数で扱えるようになれば、加算半透明ポリゴン描画のインチキな「眩しく光った」表現が、より現実に近い感じで表現できそうです。
ここで紹介したのとは別の方法ですが、違ったアプローチで制作したピンぼけフィルタ Blan'Fo Straight Version 0.3.0 を無料(フリー)のソフトウェアとして公開いたします。
(アイリスマスクと指数・対数非線形化変換を使用した Blan'Fo Straight Version 0.2 は配布を中止しました。)
指数・対数対数式を使わない方式のフィルタの風合いを、是非お楽しみ下さい。
ご興味をお持ちの方はこちらのページからどうぞ。
|
|
|